Wolf Effect

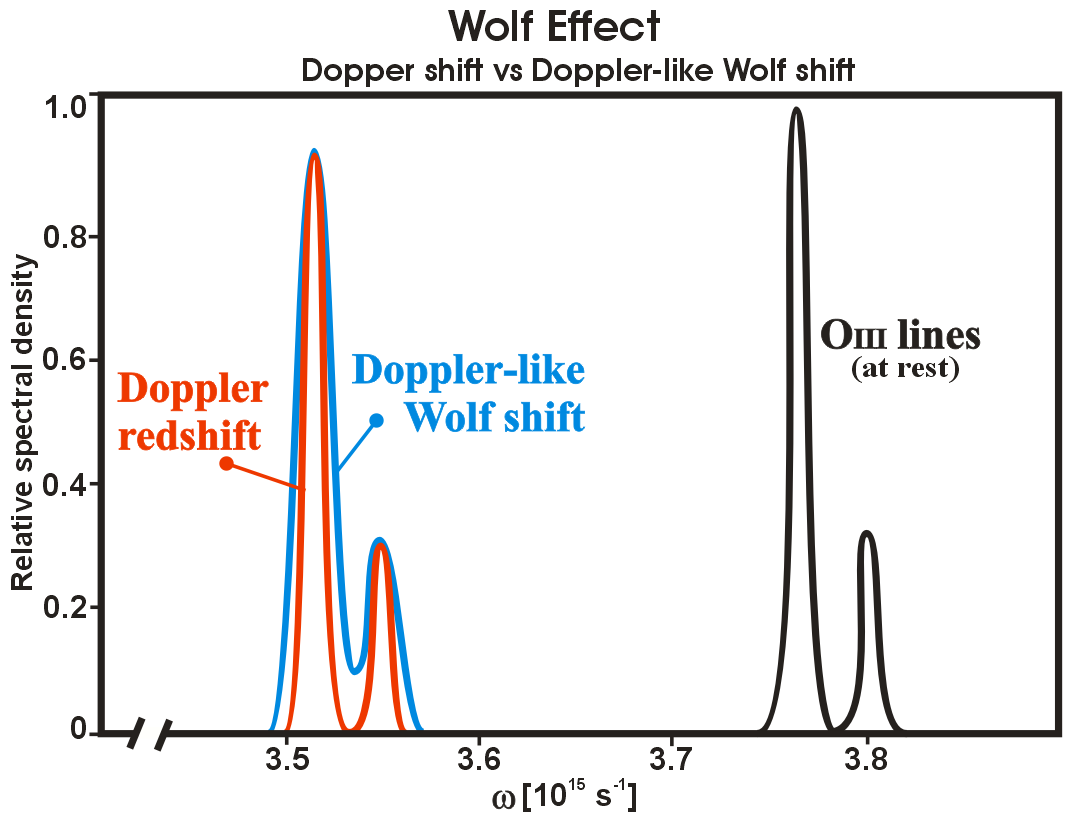
The Wolf Effect (sometimes Wolf shift) is a frequency shift in the electromagnetic spectrum, that has been described as a new redshift mechanism.^[2][3][4]
The phenomenon occurs in several closely related phenomena in radiation physics, with analogous effects occurring in the scattering of light.^[5] It was first predicted by Emil Wolf in 1987 ^{[6] [7]} and subsequently confirmed in the laboratory by Dean Faklis and George Morris in 1988 ^{[8] [9]}. Under certain conditions, the shift may be distortion free, Wolf and James write:

“A review is also presented of recent research, which has revealed that under certain circumstances the changes in the spectrum of light scattered on random media may imitate the Doppler effect, even though the source, the medium and the observer are all at rest with respect to one another. [..] This expression shows that the relative frequency shift is independent of the central frequency ω₀ of the incident light and thus imitates the Doppler effect.”^[10]

Wolf and other researchers have suggested that the Wolf effect as a possible non-cosmological redshift^[6], and also relevant to gravitational lensing,^[11] in reference to the controversies surrounding the nature of quasars that occurred in the 1970s where certain astronomers believed that quasars were local and others believed that quasars were at cosmological distances.

Theoretical description[edit]

In optics, two non-Lambertian sources that emit beamed energy can interact in a way that causes a shift in the spectral lines. It is analogous to a pair of tuning forks with similar frequencies (pitches), connected together mechanically with a sounding board; there is a strong coupling that results in the resonant frequencies getting “dragged down” in pitch.

The Wolf Effect requires that the waves from the sources are partially coherent – the wavefronts being partially in phase. Laser light is coherent while candle light is incoherent, each photon having random phase.

The Wolf Effect can produce either redshifts or blueshifts, depending on the observer’s point of view, but is redshifted when the observer is head-on.^[6] A subsequent 1999 article by Sisir Roy et al. have suggested that the Wolf Effect may explain discordant redshift in certain quasars ^[11].

For two sources interacting while separated by a vacuum, the Wolf effect cannot produce shifts greater than the linewidth of the source spectral line, since it is a position-dependent change in the distribution of the source spectrum, not a method by which new frequencies may be generated. However, when interacting with a medium, in combination with effects such as Brillouin scattering it may produce distorted shifts greater than the linewidth of the source. Under suitably controlled scenarios, it may even be possible to roughly mimic Doppler redshifts as seen in the lead figure of this article.

“Wolf outlines a more general — and perhaps physically more plausible — mechanism that could imitate Doppler shifts of any magnitude. Instead of requiring the microlamps in the source to fluctuate in some correlated fashion, he now proposes that a complex “scattering medium,” such as the electrically charged and frenetic atmosphere thought to surround quasars, might serve as an unusual lens that restructures incoming light to have redshifting or blueshifting correlations upon leaving the medium. “A scattering medium of the right type between the source and an observer should produce these effects.”^[12]

Wolf effect and Quasars[edit]

An example of such a medium which could produce Doppler-like shifts was found in 1990 by Daniel James, Malcolm Savedoff, Malcolm and Emil Wolf,^[13] and involved a highly statistically anisotropic scattering medium, that is compatible with current models of quasars. A “no blueshift” condition has also been found by Datta, S. et al., ^{[14] [15]}.

Wolf and James note ^[10] that:

“Although we make no claim that correlation-induced spectral shifts account for all, or even for a majority, of the observed shifts of lines in the spectra of extra-galactic objects, we note the possibility that correlation-induced spectral shifts may contribute to the shifts observed in the spectra of some astronomical objects such as quasars. They might help to resolve a long-standing controversy relating to pairs of astronomical objects whose spectra have different redshifts, but which appear to be physically connected, such as the pair consisting of the galaxy NGC 4319 (z = 0.006) and the quasar Markarian 205 (z = 0.007/ (Arp 1971, Sulentic 1983). The possible ‘excess’ redshift observed in the spectrum of the quasar in such a galaxy-quasar pair may perhaps be induced by the mechanism that we have just discussed”.

Sisir Roy et al write:

“.. it has been pointed out by several authors [11−13,19−21] that this mechanism may explain the anomalies in observed redshift measurements especially in the case of quasar astronomy. It is generally believed that the medium around a quasar is a highly anisotropic and plasma like (i.e., can be considered as underdense).”^[16]

Dynamic Multiple Scattering[edit]

Sisir Roy, et al, write that:

“In the last few years, a dynamic multiple scattering theory [1,2] has been developed to account for the shift as well as the broadening of spectral lines, even in the absence of any relative motion between the source and the observer. This development followed the theoretical prediction made by Wolf [3,4] who discovered that under appropriate circumstances, it is possible to have frequency shifts of spectral lines which typically mimic all the characteristics of the frequency shifts obtained by the Doppler mechanism. Since then, it has been verified by experiments [5,6] that, contrary to a commonly held belief, the spectrum of light is, in general, not invariant on propagation through a medium, especially, for anisotropic (i.e., inhomogeneous) medium with fluctuations of the dielectric susceptibility, both temporal and spatial.”^[16]

 

Notes[edit]